در ریاضیات، تابع زتای ریمان (بعد از برنارد ریمان نامگذاری شد) تابعی است بسیار مهم و پرکاربرد در نظریه اعداد . زیرا با توزیع اعداد اول رابطه دارد. همچنین کاربردهای دیگری نیز در جاهای دیگر علم دارند مانند: فیزیک، نظریه احتمال و کاربرد استاتیک.
تابع زتاریمان (ζ(s برای هر عدد مختلط s با (با جزء حقیقی بزرگتر از یک) با سری نامتناهی زیر تعریف میشود:
در ناحیه ی {s ∈ C: Re(s) > 1}, این سری همگراست و یک تابع تحلیلی در این ناحیه تعریف می کند. برنارد ریمان دریافت که چگونه میتوان این تابع را به تمام نقاط مختلط با جزء حقیقی غیر یک بسط داد که حاصل آن یک تابع مرومورفیک(ζ(s است. موقعیت صفرهای این تابع تحلیلی موضوع حدس ریمان است. بنا به این حدس، برای تمام صفرهای نابدیهی این تابع تحلیلی (آنهایی که یک عدد صحیح زوج منفی نیستند)، جزء حقیقی برابر ½ است.
[ویرایش] رابطه با اعداد اول
ارتباط این تابع با اعداد اول ابتدا توسط لئونارد اویلر پیدا شد او پی برد :
یک محاسبه نامحدود که همه اعداد اول را در بر می گیرد، نتیجه این محاسبات برای همگراست. این یک نتیجه منطقی از دو نمونه و نتیجه بنیادی در ریاضیات است. این فرمول برای سری های ژئومتریک و یک قضیه بنیادی علم حساب است.
[ویرایش] خواص متفاوت
برای تابع زتاریمان روی نوار بحرانی، تابع Z دیده می شود. برای مجموع اعداد صحیح که در تابع زتا گرفتار می شوند، سری ز تا را مستدل می کند.
[ویرایش] مقادیر ویژه
در پایین بیشترین استفاده از مقادیر تابع زتاریمان که عمومیت دارند نشان داده می شود.
; تابع هارمونیک:
; بسل]].
; ثابت آپری]]
[ویرایش] صفرهای تابع زتاریمان
تابع زتاریمان در اعداد صحیح منفی صفر دارد (به معادله ی تابع توجه کنید) به این صفرها، صفرهای بدیهی گویند انها فقط جزئی اند به این خاطر اثبات وجود آنها آسان است. برای مثال از رابطه گاما که در پایین امده است. صفرهای غیر بدیهی که در نظر گرفته می شود بیشتر با توجه به دلیل اینکه توزیع آنها نه تنها کم قابل درک است حتی مهمتر از آن اینست که به صورت حیرت آوری رگه ای در پرسش های ریاضی باز می کند. می دانیم که هر صفر غیر بدیهی تابع زتاریمان در نوار باز {s ∈ C: 0 < Re(s) < 1}, که نوار بحرانی نام دارد. فرضیه ریمان اظهار می دارد که هر صفر غیر بدیهی دارای Re(s) = 1/2 است. در قضیه تابع زتاریمان، {s ∈ C: Re(s) = 1/2} خط بحرانی نامیده می شود. جایگاه صفرهای تابع زتاریمان، اهمیت بسیاری در نظریه اعداد دارد. از حقیقت اینکه تمام صفرهای غیر بدیهی در نوار بحرانی قرار دارند، یک می توان نظریه اعداد اول را استنتاج کرد. و یک نتیجه بهتر اینست که:
قوی ترین نتیجه از این بحث اینست که را می توان درستی نظریه ریمان را انتظار داشت که نتایج بسیار ژرفی در نظریه اعداد دارد. این معلوم است که تعداد نامتناهی نوار بحرانی وجود دارد. تیهلد نشان داد که اگر دنباله (γn) قسمت موهومی و همه صفرهای صفحه بالایی را شامل می شود که:
قضیه نوار بحرانی ادعا می کند که درصد مثبتی از صفرهای غیر بدیهی در نوار بحرانی قرار دارد. در نوار بحرانی، صفر با کوچکترین قسمت موهومی غیر منفی 1/2+i14.13472514... مستقیماً از معادله ی تابعی دیده می شود که صفر غیر بدیهی متقارن اند حول Re(s) = 1/2 اگر چه ζ(s)=ζ(s*)* برای تمام اعداد مختلط s ≠ 1 بکار می رود که صفرهای تابع زتاریمان حول قسمت حقیقی متقارن و موجودند. گادفری هرلد هاردی اثبات کرد تباع زتای ریمان بینهایت صفر دارد.(هاورد و. ایوز، صفحهٔ ۲۵۸)
[ویرایش] معادله ی تابع
تابع زتا، معادله ی تابع ای که در مقابل می آید را مشخص می کند.

که برای تمام s های در C\{0,1}. معتبر است (صدق می کند)، در اینجا منظور از Γ همان تابع گاماست این فرمول برای ساختن آنالیز پیوسته بکار می رود. در S = 1، تابع زتا مانند مانده در قطب 1 است. معادله همچنین نشان می دهد که تابع زتا، صفر بدیهی از -2 , -4 , … دارد. همچنین وجود دارد نمونه ای متقارن از معادله ی تابع که در همان تعریف اولیه را می دهد
این معادله بهوسیله ی این معادله بدست آمده است:
[ویرایش] معکوس
معکوس تابع زتا از سری دریکله روی معادله ی موبیدس نتیجه می شود.
برای هر عدد مختلط s با . ، وجود دارد عددی، از رابطه مشابه که مستلزم اعداد متفاوت است که مشخص می کند تابع ضربی را که محاسبات ریاضیات را روی سری دریکله می دهد. در بالا و با بیان تعارف برای ζ(2), می توان برای حل امتحان دو پیشامد که عدد صحیح را می دهد استفاده کرد که برابر 6/π2 است. فرض ریمان هم ارز است با این ادعا که اظهار می کند که وجود دارد وقتی که . است.
[ویرایش] تابع زتاریمان از تبدیل ملین
تبدیل ملین از یک تابع fe (x) به صورت زیر تعریف می شود.
در ناحیه ای که انتگرال تعریف می شود، تعبیرهای متفاوتی برای تابع زتا در تبدیل ملین وجود دارد. اگر قسمت حقیقی S بزرگتر از 1 باشد داریم:

با حذف جمله اول بسط سری توانی از 1/(exp(x)& حول صفر، ما می توانیم در دیگر نواحی نیز تابع زتا را بدست آوریم با جزئیات در نوار بحرانی خواهیم داشت:
و وقتی قسمت حقیقی بین 0 , -1 باشد داریم:
و ما می توانیم همچنین پیدا کنیم جملاتی را که با اعداد اول رابطه دارند. اگر π(x) یک تابع محاسبه اعداد اول باشد پس
برای مقادیری با . می توانیم رابطه ای بالا را با تبدیل ملین از π(x) by پیدا کنیم.
که
یک مشابه تبدیل ملین مستلزم اینست که تابع J(x) محاسبه ای اعداد اول ریمان که اعداد ( pn ) اول توانی را محاسبه می کند با وزن 1/nپس. حال داریم:
فرمول این تعبیر می تواند برا حل تئوری اعداد اول استفاده شود. بهوسیله ی معکوس تبدیل ملین کارکردن با تابع محاسبه اعداد اول ریمان آسانتر است و می تواند با استفاده از آن بهوسیله معکوس مربیوس بهبود یابد.








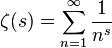















 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (بوک مارک ها)