مسئله فروشنده دورهگرد (به انگلیسی: Travelling salesman problem ، بهاختصار: TSP )
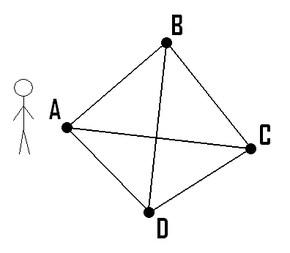
اگر فروشنده دورهگرد از نقطه A شروع کند و فواصل بین نقاط مشخص باشد، کوتاهتربن مسیر که از تمام نقاط یکبار بازدید میکند و به A بازمیگردد کدام است؟
........
مسئله فروشنده دوره گرد TSP یکی از مسائل مهم در زمره تئوری پیچیدگی محاسباتی الگوریتم ها می باشد که در گروه NP-Hard قرار می گیرد این مسئله اولین بار توسط دو دانشمند به نام های 1- هامیلتون ایرلندی و 2- کیرکمن بریتانیایی مطرح شد . معمولا بحث در خصوص این تئوری در مطالب اولیه دروس ریاضیات دانشجویان ریاضی ارائه می شود و در دروسی نظیر تئوری گراف می توانید مطالب مشابه را نیز بدست آورید .
طرح مسئله
تعدادی شهر داریم و هزینه (مسافت) مسافرت به هر یک از آنها مشخص است به دنبال کم هزینه ترین مسیر هستیم بطوریکه از همه شهرها فقط یکبار عیور کنیم و مجددا به محل شروع بازگردیم
پیچیدگی محاسباتی الگوریتم فروشنده دوره گرد
این الگوریتم بطور مستقیم در مرتبه زمانی(!O(n حل می شود اما اگر به روش برنامه نویسی پویا برای حل آن استفاده کنیم مرتبه زمانی آن (O(n^2*2^n خواهد شد که جز مرتبه های نمایی است. باید توجه داشت علی رغم آنکه مرتبه نمایی مذکور زمان بسیار بدی است اما همچنان بسیار بهتر از مرتبه فاکتوریل می باشد .
..............
شبه کد الگوریتم فوق بصورت زیر است که در آن تعداد زیر مجموعه های یک مجموعه n عضوی 2 به توان n می باشد
و for اول یک ضریب n را نیز حاصل می شود که به ازای تمام شهرهای غیر مبدا می باشد و حاصل (n*(2^n را پدید می آورد
بنابراین برای جستجوی کمترین مقدار نیاز به یک عملیات خطی از مرتبه n داریم که در زمان فوق نیز ضرب می شود و در نهایت زمان (n^2)*(2^n) را برای این الگوریتم حاصل می کند
كد:
C({1},1) = 0 for (S=2 to n ) for All Subsets S subset of {1,2,3,...} of size S and containing 1 C(S,1) = & for All J member of S , J<>1 C ( S , J ) = min { C ( S - { J } , i ) + D i,J : i member of S , i <> J } return min j C ( {1 . . . n}, J ) + D J,1
.............
اين مسئله ، مسئلهای مشهور است که ابتدا در سده ۱۸ مسائل مربوط به آن توسط ویلیام همیلتون و توماس کرکمن مطرح شد و سپس در دهه ۱۹۳۰ شکل عمومی آن به وسیله ریاضیدانانی مثل کارل منگر از دانشگاه هاروارد و هاسلر ویتنی از دانشگاه پرینستون مورد مطالعه قرار گرفت.
شرح مسئله بدین شکل است:
تعدادی شهر داریم و هزینه رفتن مستقیم از یکی به دیگری را میدانیم. مطلوب است کمهزینهترین مسیری که از یک شهر شروع شود و از تمامی شهرها دقیقاٌ یکبار عبور کند و به شهر شروع بازگردد.
تعداد کل راهحلها برابر است با برای n>۲ که n تعداد شهرها است. در واقع این عدد برابر است با تعداد دورهای همیلتونی در یک گراف کامل با n رأس.
مسئلههای مرتبط
مسئله معادل در نظریه گراف به این صورت است که یک گراف وزندار کامل داریم که میخواهیم کموزنترین دور همیلتونی را پیدا کنیم.
مسئله تنگراه فروشنده دورهگرد (به انگلیسی: Bottleneck traveling salesman problem، بهاختصار: bottleneck TSP ) مسئلهای بسیار کاربردی است که در یک گراف وزندار کموزنترین دور همیلتونی را میخواهد که شامل سنگینترین یال باشد.
تعمیمیافته مسئله فروشنده دورهگرد دارای ایالتهایی است که هر کدام حداقل یک شهر دارند و فروشنده باید از هر ایالت دقیقاٌ از یک شهر عبور کند. این مسئله به « مسئله سیاستمدار مسافر» نیز شهرت دارد.
الگوریتمها
مسئله فروشنده دورهگرد جزء مسائل NP-hard است. راههای معمول مقابله با چنین مسائلی عبارتند از:
طراحی الگوریتمهایی برای پیدا کردن جوابهای دقیق که استفاده از آنها فقط برای مسائل با اندازه کوچک صورت میگیرد.
استفاده از الگوریتمهای مکاشفهای که جوابهایی بهدست میدهد که احتمالاٌ درست هستند.
پیدا کردن زیرمسئلههایی از مسئله یعنی تقسیم مسئله به مسئلههای کوچکتر تا بشود از الگوریتمهای مکاشفهای بهتر و دقیقتری ارائه کرد.
الگوریتمهای دقیق
سرراست ترین راه حل امتحان کردن تمامی جایگشتهای ممکن برای پیدا کردن ارزانترین مسیر است که چون تعداد جایگشتها !n است، این راه حل غیرعملی میشود. با استفاده از برنامهنویسی پویا مسئله میتواند با مرتبه زمانی n22n حل شود. راههای دیگر استفاده از الگوریتمهای انشعاب و تحدید برای ۴۰ تا ۶۰ شهر، استفاده از برنامهنویسی خطی برای کوچکتر از ۲۰۰ شهر و استفاده از روش برش-صفحه برای اندازههای بزرگ است.
الگوریتمهای مکاشفهای
الگوریتمهای تقریبی متنوعی وجود دارند که خیلی سریع جوابهای درست را با احتمال بالا بهدست میدهند که میتوان آنها را به صورت زیر دستهبندی کرد:
مکاشفهای سازنده
بهبود تکراری
مبادله دوبهدو
مکاشفهای k-opt
مکاشفهای V-opt
بهبود تصادفی







 پاسخ با نقل قول
پاسخ با نقل قول



علاقه مندی ها (بوک مارک ها)