شما آینه محدب را در پیچ جاده ها، در فروشگاه های بزرگ و در آینه بغل ماشین مشاهده كرده اید. آیا به نحوه تشكیل تصویر در آن ها فكر كرده اید؟
در زیر پرندهای در مقابل آینه محدب قرار گرفته است سعی كنید محل پرنده را جابه جا كنید محل تصویر در جلوی آینه است یا پشت آینه؟
اندازه تصویر همیشه بزرگتر از پرنده است یا كوچكتر از آن؟
جهت مشاهده مدل سازی این جا را کلیک کنید و فایل index را بازکنید.
برای یافتن محل تصویر مجازی، مشابه قبل، رسم مسیر دو پرتو خارج شده از راس شی كافی است.
شئ: در مقابل آینه محدب
تصویر: بین آینه و كانون (پشت آینه)
كوچكتر مستقیم مجازی
در صورتی كه فاصله شئ تا آینه را با علامت ( p) و فاصله تصویر تا آینه را با علامت ( q ) و فاصله كانونی آینه را با علامت f ) ) مشخص كنیم ، رابطه زیر بین این كمیت ها بر قرار است:
1/p + 1/q = 1/f
نكته مهم !
در رابط فوق، كمیت های حقیقی دارای علامت مثبت و كمیت های مجازی دارای علامت منفی است.
مثلا هر گاه در یك مسئله، مقدار q منفی باشد، تصویر مجازی خواهد بود.
كانون آینه مقعر، حقیقی و مثبت است زیرا كه حقیقتا بازتاب پرتو های موازی در كانون آن جمع می شوند ولی كانون آینه محدب، مجازی و منفی است زیرا كه امتداد بازتاب پرتو های موازی از كانون آن می گذرد.
برای علاقمندان به دانستن بیشتر!
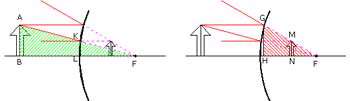
در شكل فوق دو مثلث ABF و KLF با یكدیگر متشابه اند. از این تشابه تساوی (1) نتیجه می شود.
1) AB / KL =BF / LF
در این شكل دو مثلث GHF و MNF با یكدیگر متشابه اند. از این تشابه تساوی (2) نتیجه می شود.
2) GH / MN =HF / NF
از آنجا كه KL = MN و AB = GH ، تساوی های (1) و (2) به صورت زیر در می آید:
3) AB / MN =BF / LF
4) AB / MN =HF / NF
با تركیب تساوی های (3) و (4) ، تساوی (5) حاصل می شود.
5) BF / LF =HF / NF
قدم بعدی آن است كه به جای هر یك از چهار پاره خط شركت كننده در رابطه (5) ، مقدار آن ها را بر حسب p (فاصله شئ تا آینه) ، q (فاصله تصویر تا آینه) وf (فاصله كانونی یا نصف شعاع آینه) قرار دهیم.
با دقت در شكل و ناچیز فرض كردن اثر انحنای آینه، چهار رابطه زیر به دست می آید:
BF = BL + LF = p +f
LF = f
HF = f
NF = HF -NH = f -q
بنابراین، تساوی (5) به صورت زیر در می آید:
( p + f ) / f = f / ( f -q )
با ضرب طرفین و وسطین تساوی فوق، تساوی زیر به دست می آید:
pf -pq -fq + ff = ff
با ساده كردن، رابطه زیر به دست می آید:
qf - pf = - pq
با تقسیم دو طرف این تساوی بر pqf ، تساوی مهم زیر به دست می آید:
در صورتی كه به دلیل مجازی بودن، علامت منفی در خود مقادیر q و f در نظر گرفته شود، تساوی به صورت زیر در می آید:








 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (بوک مارک ها)