اعداد هگزادسیمال
برای راحتی محاسبات در کامپیوترها از سیستم اعداد هگزادسیمال، یعنی اعداد در مبنای 16 استفاده می شود. چقدر با این محاسبات آشنایی دارید؟سیستم اعداد باینری دارای دو رقم 0 و 1 می بلشند، ولی سیستم اعداد دهدهی از رقم های 0 تا 9 تشکیل می شوند و سیستم اعداد هگزادسیمال دارای رقم های 0 تا 9 و رقم های A و B و C و D و E و F می باشد. به عنوان مثال عدد باینری 100010010110 که از یک سری 0 و 1 تشکیل شده را می توان به صورت 896 H هگزادیسمال که خواندنش آسان تر است، نشان داد.
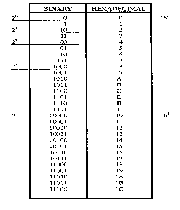
در جدول زیر میتوانید معادل اعداد دسیمال، هگزادسیمال و باینری را مشاهده کنید.
تبدیل اعداد باینری به هگزادسیمال
هما طور که گفتیم پایه اعداد هگزادسیمال، 2^4 = 16 است که این عدد معادل چهار بین باینری می باشد، پس برای تبدیل اعداد باینری به هگزادسیمال کافیست عدد باینری را از سمت راست، چهار بیت چهار بیت جدا کنیم و به جای هر چهار بیت، کد معادل نظیر هگزادسیمال آن را قرار دهیم.
به عنوان مثال عدد باینری 1010111101100011 را با یکدیگر به مبنای هگزادسیمال تبدیل می کنیم. به سادگی چهار بیت چهار بیت از سمت راست جدا می کنیم و خواهیم داشت :
(0011)(0110)(1111)(1010)برای هر پرانتز معادل باینری آن را می نویسم:
(0011)= 3 ، (0110)=6 ، (1111)=F، (1010)=Aبنابراین عدد باینری فوق، معادل عددH AF63 در سیستم هگزادسیمال است. علامت H در انتهای عدد نشان دهنده سیستم اعداد هگزادسیمال است. در صورتی که در انتهای سمت چپ عدد، کمتر از 4 بیت باقی ماند، به انتهای سمت چپ عدد آنقدر صفر اضافه می کنیم تا گروه آخری هم چهار بیتی شود که بتوان معادل هگزادسیمال آن را نوشت.
برای تبدیل اعداد هگزا دسیمال به باینری نیز تنها کافیست عملایت بالا را به صورت معکوس انجام دهید. به این ترتیب که برای هر رقم هگزا، معادل باینری آن را نوشته و جواب نهایی را محاسبه کنید. به عنوان مثال عدد 8E6 H برابر است با:
8 = 1000 , E = 1110 , 6 = 0110که در نهایت معادل است با عدد 100011100110 باینری.
برای تبدیل اعداد هگزادسیمال به دهدهی و برعکس، همان طور که در تبدیلات باینری توضیح داده شد عمل می کنیم. به این ترتیب که برای تبدیل به دهدهی هر رقم را در وزن ارزش مکانی خود ضرب کرده و حاصل را جمع می کنیم. برای تبدیل از دهدهی به هگرادسیمال نیز از تقسیمات متوالی بر 16 تا جایی که خارج قسمت 0 شود، استفاده می کنیم.
جمع هگزادسیمال
برای جمع اعداد هگزادسیمال از کوچکترین رقم سمت راست شروع می کنیم. اگر مجموع دو رقم کوچکتر از رقم 16 بود، آن رقم را می نویسیم و اگر بزرگتر از 16 بود، عدد 16 را از آن کم می کنیم و عدد هگزادسیمال معادل را بدست آورده و یک بیت نقلی برای اضافه کردن به رقم بعدی در نظر می گیریم.
برای درک بهتر دو عدد 834B و 23D9 را جمع می کنیم.
از کوچکترین رقم مجموع شروع می کنیم. 9 + B = 9 + 11 = 20. 20 از 16 بزرگتر است پس 20 – 16 = 4 و نتیجه جمع دو رقم را برابر 4 قرار می دهیم و یک بیت نقلی به رقم بعدی اضافه می کنیم.
برای رقم بعدی داریم 1 + D + 4 = 1 + 13 + 4 = 18. مانند مرحله قبل از 16 بزرگتر است پس 18 – 16 = 2. پس مجموع را برابر 2 قرار می دهیم و یک بین نقلی به رقم بعدی اضافه می کنیم.
برای رقم بعدی خواهیم داشت 1 + 3 + 3 = 7. عدد 7 در سیستم هگزا قابل قبول است و بدون تغییر باقی می ماند.
در نهایت برای رقم آخر 2 + 8 = A که عدد A هم قابل قبول است و بدون تغییر باقی می ماند.
بنابراین مجموع دو عدد برابر A724 هگزادسیمال می شود.
تفریق هگزادسیمال
مانند تفریق دهدهی عمل می کنیم. با این تفاوت که به جای قرض گرفتن عدد 10 ، از عدد 16 استفاده می کنیم. در تفریق اگر رقم مفروق کوچکتر از مفروق منه باشد، باقیمانده یک رقم هگزادسیمال است ولی اگر رقم مفروق بزرگتر از مفروق منه باشد، عدد 16 را به رقم مفروق منه اضافه کرده و یک بیت نقلی از رقم بعدی قرض می گیریم.
فاطمه مجدآبادی
بخش دانش و زندگی تبیان








 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (بوک مارک ها)