تابع اولیه
هر گاه معادله مشتق تابعی معلوم باشد وبخواهیم معادله اصلی تابع را تعیین کنیم این عمل را تابع اولیه می نامیم.
تعریف: تابع اولیه y = f(x)را تابعی مانند Y = F(x) + c می نامیم،هرگاه داشته باشیم:
cعدد ثابت (y = F(x) + c)' = y = f(x)
انتگرال نامعین
تعریف:هرگاه معادله دیفرانسیلی تابعی معلوم باشد وبخواهیم معادله اصلی تابع را معلوم کنیم این عمل راانتگرال نا معیین نامیده و آن را با نمادنمایش میدهند.
بنا به تعریف نمادرا انتگرال نامعین نامیده وحاصل آن را تابعی مانندF(x) + c در نظر میگیریم هر گاه داشته باشیم:
با شرط: (F(x) + c)' = f(x)
انتگرال معین
بنا به تعریف نمادرا انتگرال معین نامیده و حاصل آن را عددی به صورت زیر تعریف میکنیم: a<x<b
aوb را به ترتیب کرانهای بالا و پایین انتگرال مینامیم.
تابع انتگرالپذیر
اگر تابعی دارای انتگرال باشد به آن انتگرالپذیر گویند.
تعبیر هندسی انتگرال
از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.
نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سهگانه معرف پارالل زیر نمودار است(غیرقابل تصور).
مثال
انتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی fx است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.

نمایش گرافیکی انتگرال.
انتگرال یک تابع مساحت زیر نمودار آن تابع است.
انتگرال گیری
(محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است.
مهمترین تعاریف در انتگرال
از مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است. انتگرال ریمان بهوسیله برنهارد ریمان در سال 1854 ارائه شد که تعریف دقیقی را از انتگرال ارائه میداد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعويض پذيری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه میکرد. از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال ریمان-استیلچس (Riemann-Stieltjes) اشاره کرد. پس به طور خلاصه سه تعریف زير از مهمترين تعاريف انتگرال مي باشند:
- انتگرال ريمان
- انتگرال لبگ
- انتگرال ریمان-استیلتیس (تعمیم انتگرال ریمان)
کاربرد
انتگرال ها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک میتوان برای کاربرد های زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست میآید. اما به طور کلی میتوان آن را تغییرات کمیت حاصل ضرب افقی و عممودی نمودار نامیدمثلا: در یک رابطه کمیت ها را تحلیل ابعادی می کنیم مثلا رابطه سرعت و زمان را به صورت زیر نوشته میشود:
سپس دو تحلیل را در هم ضرب می کنیم:
پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.
ویکی پدیا









 پاسخ با نقل قول
پاسخ با نقل قول




 ,
,  , this is related to the
, this is related to the 





















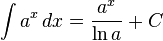



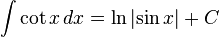

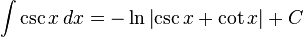






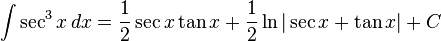
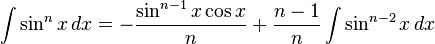















 (see also
(see also  (the
(the  (see also
(see also 

 (if n is an even integer and
(if n is an even integer and  )
)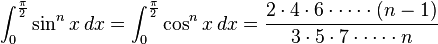 (if
(if  is an odd integer and
is an odd integer and 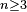 )
)
 (where Γ(z) is the
(where Γ(z) is the 
 یا
یا  نمایش میدهند.
نمایش میدهند.
 انتگرال سه گانه:معرف پارالل زیر نمودار(می توان آن را نوعی حجم ضربدر زمان گرفت) است مثلا
انتگرال سه گانه:معرف پارالل زیر نمودار(می توان آن را نوعی حجم ضربدر زمان گرفت) است مثلا
 ) که در شرایط انتگرال خطی دارای پیوستگی طبیعیاند (برای مثال
) که در شرایط انتگرال خطی دارای پیوستگی طبیعیاند (برای مثال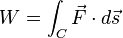 ) ). این انتگرال کاری را که روی حرکت شی در میدان گرانشی انجام میدهد، بدست میآورد.
) ). این انتگرال کاری را که روی حرکت شی در میدان گرانشی انجام میدهد، بدست میآورد. R انتگرال خطی روی منحنی C با پارامتریزه شدن r(t) که:
R انتگرال خطی روی منحنی C با پارامتریزه شدن r(t) که: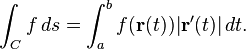
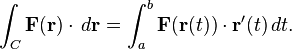 انتگرال خطی میدانها برداری به پارامتریزه شدن (r(t وابستهاند و مقدار اصلی آنها وابسته به جهت آنهاست. به ویژه اگر جهت انتگرال عوض شود، مقدار متمایزی به ما میدهد.
انتگرال خطی میدانها برداری به پارامتریزه شدن (r(t وابستهاند و مقدار اصلی آنها وابسته به جهت آنهاست. به ویژه اگر جهت انتگرال عوض شود، مقدار متمایزی به ما میدهد. پس یک مشتق از ترکیب G و (r(t هست که
پس یک مشتق از ترکیب G و (r(t هست که که مقداری برای انتگرال خطی از میدان F روی (r(t است. با دنبالهروی از این روش، یک مسیر روی C به ما میدهد که
که مقداری برای انتگرال خطی از میدان F روی (r(t است. با دنبالهروی از این روش، یک مسیر روی C به ما میدهد که در لغت، انتگرال F روی C فقط وابسته به مقادیر نقاط (r(a و (r(b است. بدین گونه مستقل از راهها و جهتهای متفاوت است. بنابراین یک میدان برداری که از گرادیان یک میدان اسکالر بدست آمده است، راه استقلال مینامند.
در لغت، انتگرال F روی C فقط وابسته به مقادیر نقاط (r(a و (r(b است. بدین گونه مستقل از راهها و جهتهای متفاوت است. بنابراین یک میدان برداری که از گرادیان یک میدان اسکالر بدست آمده است، راه استقلال مینامند.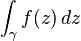 . بازه [a,b] را به صورت زیر افراز میکنیم.
. بازه [a,b] را به صورت زیر افراز میکنیم. انتگرال بالا برابر حد مجموع بالاست که طول زیرمجموعهها به سمت صفر میل میکند. اگر یک منحنی متغیر باشد، انتگرال خطی میتواند محاسبه کند، به طوری که انتگرال تابع با مقادیر حقیقی باشد.
انتگرال بالا برابر حد مجموع بالاست که طول زیرمجموعهها به سمت صفر میل میکند. اگر یک منحنی متغیر باشد، انتگرال خطی میتواند محاسبه کند، به طوری که انتگرال تابع با مقادیر حقیقی باشد. وقتیγ یک منحنی بسته باشد مقدار اولیه و مقدار آخری با هم روی میدهد که آنرا با
وقتیγ یک منحنی بسته باشد مقدار اولیه و مقدار آخری با هم روی میدهد که آنرا با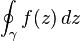 نشان میدهند که معمولاً برای انتگرال خطی f رویγ بسته نمایش داده میشود. بهترین حکم در مورد انتگرال خطی (جهتی)، قضیهی انتگرال کشی و فرمول انتگرال کشی است. زیرا با استفاده از قضیه مانده میتوان روش انتگرال خطی (جهتی) در صفحه مختلط برای پیدا کردن انتگرال و مقدار حقیقی تابع از یک متغیر حقیقی پیدا کرد.
نشان میدهند که معمولاً برای انتگرال خطی f رویγ بسته نمایش داده میشود. بهترین حکم در مورد انتگرال خطی (جهتی)، قضیهی انتگرال کشی و فرمول انتگرال کشی است. زیرا با استفاده از قضیه مانده میتوان روش انتگرال خطی (جهتی) در صفحه مختلط برای پیدا کردن انتگرال و مقدار حقیقی تابع از یک متغیر حقیقی پیدا کرد.
 که میتوان این مثال را از طریق انتگرال کشی بازبینی نمود.
که میتوان این مثال را از طریق انتگرال کشی بازبینی نمود.


علاقه مندی ها (بوک مارک ها)