انتخاب مقدار ثابت انتگرال‌گیری
در حل یک معادله دیفرانسیل مانندمعمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی
را تعیین می‌کنیم که همه جوابهای ممکن را به دست می‌دهد . سپس مقداری از
را تعیین می‌کنیم که جواب خاص مطلوب را به دست دهد.
اگر نقطه‌ای چوناز دامنه
را در نظر بگیریم و مقدار دلخواه
را برگزینیم ، می‌توان با قرار دادن
و
در معادله
بگذرد.به این ترتیب داریم
یا
.
خمخمی است که از
انتگرال‌گیری به کمک تغییر متغیر
در حل انتگرال‌ها با روش تغییر متغیر ، به جایتابع پیوسته و مشتق پذیر
را قرار می دهیم، یعنی :
بعد از حل ، بر اساس تابع معکوس ، به جاینسبت به
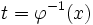
از فرمول فوق به صورت زیر هم می‌توان استفاده کرد:
انتگرال‌گیری به روش جزء به جزء
دستورموسوم به انتگرال‌گیری به روش جزء به جزء است که در آن
توابعی مشتق‌پذیر از
را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب می‌کنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را
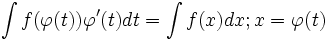
پاسخ با نقل قول
علاقه مندی ها (بوک مارک ها)