بيش از دو هزار سال پيش ارشميدس (287-212 قبل از ميلاد) فرمول هايي را براي محاسبه سطح وجه ها ، ناحيه ها و حجم هاي جامد مثل كره ، مخروط و سهمي يافت . روش انتگرال گيري ارشميدس استثنايي و فوق العاده بود جبر ، نقش هاي بنيادي ، كليات و حتي واحد اعشار را هم نمي دانست .
ليبنيز (1716-1646) و نيوتن (1727-1642) حسابان را كشف كردند . عقيده كليدي آنها اين بود كه مشتق گيري و انتگرال گيري اثر يكديگر را خنثي مي كنند با استفاده از اين ارتباط ها آنها توانستند تعدادي از مسائل مهم در رياضي ، فيزيك و نجوم را حل كنند.
فورير (1830-1768) در مورد رسانش گرما بوسيله سلسله زمان هاي مثلثاتي را مي خواند تا نقش هاي بنيادي را نشان دهد .رشته هاي فورير و جابجايي انتگرال امروزه در زمينه هاي مختلفي چون داروسازي و موزيك اجرا مي شود .
گائوس (1855-1777) اولين جدول انتگرال را نوشت و همراه ديگران سعي در عملي كردن انتگرال در رياضي و علوم فيزيك كرد . كايوچي (1857-1789) انتگرال را در يك دامنه همبستگي تعريف كرد . ريمان (1866-1826) و ليبيزگو (1941-1875) انتگرال معين را بر اساس يافته هاي مستدل و منطقي استوار كردند .
ليوويل (1882-1809) يك اسكلت محكم براي انتگرال گيري بوجود آورد بوسيله فهميدن اينكه چه زماني انتگرال نامعين از نقش هاي اساسي دوباره در مرحله جديد خود نقش اساسي مرحله بعد هستند . هرميت (1901-1822) يك شيوه علمي براي انتگرال گيري به صورت عقلي و فكري ( يك روش علمي براي انتگرال گيري سريع ) در دهه 1940 بعد از ميلاد استراسكي اين روش را همراه لگاريتم توسعه بخشيد .
در دهه بيستم ميلادي قبل از بوجود آمدن كامپيوترها رياضيدانان تئوري انتگرال گيري و عملي كردن آن روي جداول انتگرال را توسعه داده بودند و پيشرفت هايي حاصل شده بود .در ميان اين رياضيدانان كساني چون واتسون ، تيچمارش ، بارنر ، ملين ، ميچر ، گرانبر ، هوفريتر ، اردلي ، لوئين ، ليوك ، مگنوس ، آپل بلت ، ابرتينگر ، گرادشتاين ، اكستون ، سريواستاوا ، پرودنيكف ، برايچيكف و ماريچيف حضور داشتند .
در سال 1969 رايسيچ پيشرفت بزرگي در زمينه روش علمي گرفتن انتگرال نامعين حاصل كرد . او كارش را بر پايه تئوري عمومي و تجربي انتگرال گيري با قوانين بنيادي منتشر كرد روش او عملاً در همه گروه هاي قضيه بنيادي كارگر نيست تا زماني كه در وجود آن يك معادله سخت مشتق گيري هست كه نياز دارد تا حل شود . تمام تلاش ها ااز آن پس بر روي حل اين معادله با روش علمي براي موفقيت هاي مختلف قضيه اساسي گذاشته شد . ايت تلاش ها باعث پيشرفت كامل سير و روش علمي رايسيچ شد . در دهه 1980 پيشرفت هايي نيز براي توسعه روش او در موارد خاص از قضيه هاي مخصوص و اصلي او شد .
از قابليت تعريف انتگرال معين به نتايجي دست ميابيم كه نشان دهنده قدرتي است كه در رياضيات مي باشد (1988) جامعيت و بزرگي به ما ديدگاه موثر و قوي در مورد گسترش در رياضيات و همچنين كارهاي انجام شده در قوانين انتگرال مي دهد . گذشته از اين رياضيات توانايي دارد تا به تعداد زيادي از نتيجه هاي مجموعه هاي مشهور انتگرال پاسخ دهد ( اينكه بفهميم اين اشتباهات ناشي از غلط هاي چاپي بوده است يا نه ) . رياضيات اين را ممكن مي سازد تا هزاران مسئله انتگرال را حل نماييم به طوريكه تا كنون در هيچ يك از كتابهاي دستنويس قبلي نيامده باشد . در آينده ديگر وظيفه ضروري انتگرال اين است كه به ازمايش تقارب خطوط ، ارزش اصلي آن و مكانيسم فرض ها بپردازد .







 پاسخ با نقل قول
پاسخ با نقل قول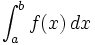 نشان می دهند علامت
نشان می دهند علامت  ،انتگرال گیری از تابع نمادی برای متغیر انتگرال گیری است. dx تابعی انتگرال پذیر است و f ابتدا و انتهای بازه هستند و یک کمیت بی نهایت کوچک dx از لحاظ تاریخی را نشان می دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی را بین f پایه گذاری شده است به عنوان مثال تابع در نظر بگیرید ،مساحت زیر x=0 تا x=10 نمودار در واقع مساحت مستطیل خواهدبود که بین محصور شده است یعنی x=0 ،x=10 ،y=0 ،y=3 دارای طول 10 و عرض 3است پس مساحت آن برابر 30 خواهد بود . انتگرال یک تابع
،انتگرال گیری از تابع نمادی برای متغیر انتگرال گیری است. dx تابعی انتگرال پذیر است و f ابتدا و انتهای بازه هستند و یک کمیت بی نهایت کوچک dx از لحاظ تاریخی را نشان می دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی را بین f پایه گذاری شده است به عنوان مثال تابع در نظر بگیرید ،مساحت زیر x=0 تا x=10 نمودار در واقع مساحت مستطیل خواهدبود که بین محصور شده است یعنی x=0 ،x=10 ،y=0 ،y=3 دارای طول 10 و عرض 3است پس مساحت آن برابر 30 خواهد بود . انتگرال یک تابع 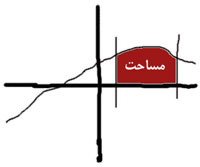
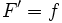 را پیدا می کنیم که تابعی است مانند f 2.پاد مشتق 3 .قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می گیریم:
را پیدا می کنیم که تابعی است مانند f 2.پاد مشتق 3 .قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می گیریم: 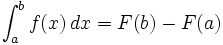
 خواهد بود.
خواهد بود.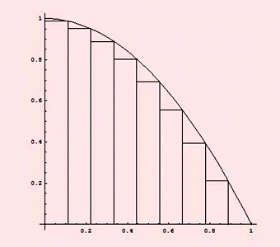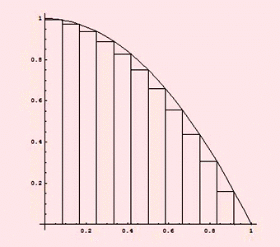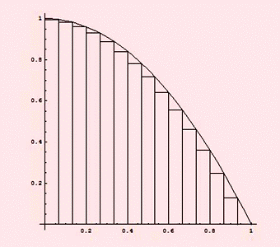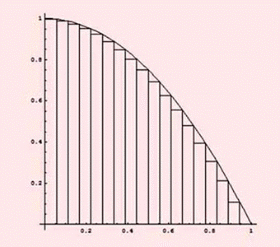
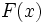 پاد
پاد 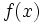 باشد ، آنگاه
باشد ، آنگاه 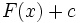 به ازای هر مقدار ثابت
به ازای هر مقدار ثابت 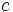 یک پاد مشتق
یک پاد مشتق 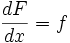 آنگاه:
آنگاه: 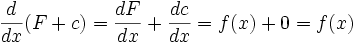
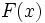 جوابی برای
جوابی برای  باشد ، فرمول
باشد ، فرمول 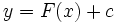 همه جوابها را به دست میدهد.
همه جوابها را به دست میدهد. 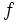 نسبت به
نسبت به 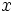 مینامند و با
مینامند و با 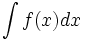 نشان میدهند.
نشان میدهند. 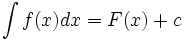
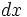 نشان میدهد که متغیر انتگرالگیری
نشان میدهد که متغیر انتگرالگیری 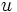 برابر است با
برابر است با 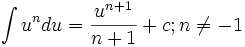
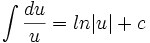
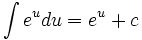 ,
, 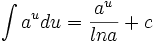
 ,
, 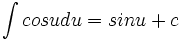
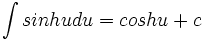 ,
, 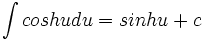
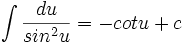 ,
, 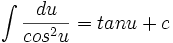
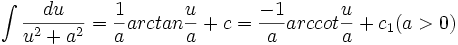
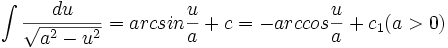
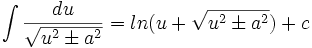
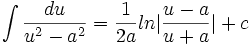
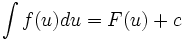 آنگاه
آنگاه 
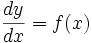 معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی
معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی 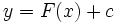 را تعیین میکنیم که همه جوابهای ممکن را به دست میدهد . سپس مقداری از
را تعیین میکنیم که همه جوابهای ممکن را به دست میدهد . سپس مقداری از 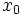 از دامنه
از دامنه 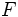 را در نظر بگیریم و مقدار دلخواه
را در نظر بگیریم و مقدار دلخواه 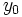 را برگزینیم ، میتوان با قرار دادن
را برگزینیم ، میتوان با قرار دادن 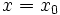 و
و 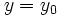 در معادله
در معادله 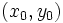 بگذرد.به این ترتیب داریم
بگذرد.به این ترتیب داریم 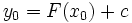 یا
یا 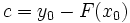 .
. 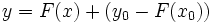 خمی است که از
خمی است که از 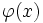 را قرار می دهیم، یعنی :
را قرار می دهیم، یعنی : 
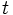 نسبت به
نسبت به 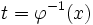
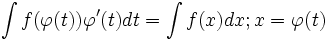
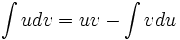 موسوم به انتگرالگیری به روش جزء به جزء است که در آن
موسوم به انتگرالگیری به روش جزء به جزء است که در آن 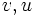 توابعی مشتقپذیر از
توابعی مشتقپذیر از 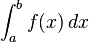 aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.
aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.


علاقه مندی ها (بوک مارک ها)