یادگیری گام به گام حد

[shirin71]

حد در ریاضیات مفهومی است برای بیان رفتار تابع در نزدیکی یک نقطه هنگامی که متغیر تابع به آن نقطه میل می‌کند.

تعریف

عبارت زیرین به اثبات اپسیلون و دلتا مشهور است که بار اول توسط ریاضیدان آلمانی کارل ویستراس عنوان شد:






به این معنی است که، برای هر یک وجود دارد، که برای هر x با خاصیت ، آنگاه داریم: .
مثال:
اثبات :
برای هر یک وجود دارد به شکلی که:
اگر 0 < x < 0 + δ
یا اگر 0 < x < δ
با گرفتن جذر هر دو سمت می‌توانیم عبارت قبلی را به شکل زیر بنوسیم:
اگر 0 < x < δ
بنا بر این δ = ε2
و این را اثبات می‌کند.

حد تابع

فرض کنید f(x)‎ تابعی حقیقی و c عددی حقیقی باشد. عبارت
‎

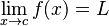
بدین معناست که f(x)‎ به ازای xهای نزدیک به c به L میل می‌کند. توجه داشته باشید که این عبارت می‌تواند صحیح باشد حتی اگر باشد. دو مثال زیر مساله را روشن‌تر بیان می‌کند. است و به x مقدار ۲ را می‌دهیم. در این مثال x در ۲ تعریف شده و مقدار تابع در آن برابر حدش ۰٫۴ است:
f(1.9) f(1.99) f(1.999) f(2) f(2.001) f(2.01) f(2.1) 0.4121 0.4012 0.4001 0.4 0.3998 0.3988 0.3882 اگر به x مقدار ۲ را بدهیم f(x)‎ برابر ۰٫۴ خواهد شد و داریم . در این مثال است اما این عبارت همواره صحیح نیست، برای مثال:
‎

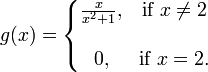
حد g(x)‎ به ازای x برابر ۲ مساوی ۰٫۴ می‌باشد اما و g در ۲ پیوسته نیست.
در مثالی دیگر فرض می کنیم که تابع در x = c تعریف نشده باشد:
‎

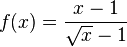
اگر به x مقدار ۲ را بدهیم تابع تعریف نشده اما حد آن برابر ۲ است:
f(0.9) f(0.99) f(0.999) f(1.0) f(1.001) f(1.01) f(1.1) 1.95 1.99 1.999 تعریف نشده 2.001 2.010 2.10
منبع

‎

• Carl B. Boyer, A history of mathematics, 2nd edition, by John Wiley & Sons, Inc., 1991
• ویکی پدیا