به عنوان یک تجزیه و فاکتورگیری ماتریسی، تجزیۀ مقدارهای منفرد یا تجزیۀ مقدارهای تکین (Singular value decomposition) قدمی اساسی در بسیاری از محاسبات علمی و مهندسی بهحساب میآید.
فرض کنیم M یک ماتریس m در n روی میدان K است که می تواند یکی از میدان های حقیقی یا مختلط باشد. آنگاه تجزیه ای از M به صورت زیر وجود دار:
که U یک ماتریس m در n روی میدان Σ ، K ماتریس قطری m در n با درایه های نا منفی حقیقی بر روی قطر و V* نشاندهنده ترانهاده مزدوج V یک ماتریس یکانی n در n روی K است. این روش فاکتور گیری تجزیه مقدارهای منفرد M نامیده می شود.
قرارداد: ماتریس قطری Σ به طور منحصر بفرد به وسیله M تعیین می شود.(اگرچه ماتریس های U و V اینگونه نیستند) . درایه های ماتریس قطری Σ به عنوان مقدارهای تکین M شناخته می شوند.
ماتریس زیر را در نظر میگیریم:
یکی از تجزیۀ مقدارهای منفرد این ماتریس به صورت زیر است:
یعنی داریم که








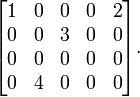


 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (بوک مارک ها)