تئوري ريسمان به زبان سادهرشته سيمهاي گيتار را تصور كنيد كه با كشيده شدن در طول گيتار كوك شدهاند؛ بسته به آنكه سيمها چقدر كشيده شوند و تحت فشار قرار گيرند، نتهاي موسيقي مختلفي بوسيله آنها ايجاد ميشود. ميتوانيم اين نتهاي موسيقي را «حالتهاي برانگيخته» سيمهاي گيتار تحت كشش بناميم.
به طور مشابه در تئوري ريسمان ذرات بنيادين كه در شتابدهندهها مشاهده ميشوند را ميتوانيم نتهاي موسيقي و يا همان «حالتهاي برانگيخته» فرض گنيم.
در تئوري ريسمان همانند نواختن گيتار، ريسمانها بايد تحت كشش قرار بگيرند تا برانگيخته شوند. اگرچه ريسمانها در تئوري ريسمان در فضا-زمان شناور هستند و مانند گيتار مقيد نيستند وليكن با اين حال آنها كشش دارند، كشش ريسمان در تئوري ريسمان همانطور كه در قبل گفتيم با كميت :شناخته ميشود و در آن ´a با مربع مقياس طول ريسمان متناسب است.
اگر تئوري ريسمان تئوري گرانش كوانتوم باشد، پس متوسط اندازه ريسمان بايد چيزي نزديك به مقياس طول گرانش كوانتوم باشد كه طول پلانك ناميده ميشود و حدود 10-33 سانتيمتر ميباشد. متاسفانه اين بدان معناست كه ريسمانها به حدي براي ديدن با تكنولوژي فعلي فيزيك ذرات كوچك هستند كه فيزيكدانان مجبور به ابداع روشهاي جديدي براي آزمايش تئوري شدند.
تئوري در ابتدا فقط براي بوزونها بود، به منظور اينكه فرميونها هم وارد تئوري ريسمان شوند بايد يك نوع بخصوص از تقارن به نام ابرتقارن وجود ميداشت كه به واسطه آن براي هر بوزون، يك فرميون متناظر وجود داشته باشد. پس ابرتقارن، ذرات حامل نيرو و ذراتي كه ماده را ميسازند به هم مربوط ميكند.
نتايج ابرتقارن در آزمايشات ذرات مشاهده نشدهاند اما تئوريستها معتقد هستند كه ذرات ابرتقارن بزرگتر و سنگينتر از آن هستند كه در شتابدهندههاي فعلي بتوان آنها را مشاهده كرد. ايجاد شتابدهندههاي قويتر انرژي بالا در دهه آينده ميتواند شواهد لازم براي ابرتقارن در اختيار ما قرار دهند.
مهم نبود كه هر كس چقدر تلاش ميكرد، به نظر ميرسيد گرانش به هيچ وجه به نظريهاي قابل بهنجارش تبديل نميشود؛ يك مشكل بزرگ اين بود كه امواج گرانش كلاسيك كه فرض ميشد ذره حامل آن گراويتون است، داراي اسپين 2 بودند و براي اسپين 2 ، عبارت 4j-8+D مساوي D ميشد و براي D=4 ، انتگرال بينهايت ميشد، مثل توان چهارم ممنتوم وقتي كه ممنتوم به سمت بينهايت ميل ميكند.
و اين براي فيزيكدانان غيرقابل هضم بود و سالها تلاش آنها در راه رسيدن به «گرانش كوانتوم» ناكام ماند.
در اينجا بود كه تئوري ريسمان وارد شد تا اين خلا را پر كند.
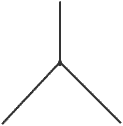
تئوري ريسمان در اصل براي توصيف روابط ميان جرم و اسپين هادرونها پيشنهاد شده بود. در تئوري ريسمان، ذرات از برآشفتگي ريسمانهاي بسيار ريزي بوجود ميآمدند ؛ يك ذره كه از اين برآشفتگيها بر ميخواست، ذرهاي بود با جرم صفر و دو واحد اسپين.
موفقيتي كه تئوري ريسمان داشت اين بود كه در مدل دياگرامهاي فاينمن، دياگرامها به سطوح صاف دو بعدي تبديل ميشدند و انتگرالهاي روي سطح ديگر مشكل فاصله صفر را نداشتند.
تئوري ذرهاي :تئوري ريسمان :در 1974 نهايتا اين سوال مطرح شد كه " آيا تئوري ريسمان ميتواند تئوري گرانش كوانتوم باشد؟ ".
در تئوري ريسمان، ممنتوم بينهايت به معناي فاصله صفر نبود، زيرا در اين تئوري رابطه بين ممنتوم و فاصله به قرار زير بود:كميت 'a به تنش ريسمانها بستگي داشت ، كميتي بنيادين بر اساس رابطه :رابطه بالا به طور غيرمستقيم بيان ميكند كه كمترين طول قابل مشاهده براي تئوري ريسمان به صورت زير است:رفتار ذره در فاصله صفر كه در تئوري ميدان كوانتوم بسيار مشكلساز بود، در تئوري ريسمان بسيار بياهميت شد و همين باعث شد كه تئوري ريسمان نامزد تئوري گرانش كوانتوم شود.
اگر تئوري ريسمان ، تئوري گرانش كوانتوم باشد، مقدار طول مينيموم بايد حداقل اندازه طول پلانك باشد كه از تركيب ثابت پلانك و ثابت گرانش نيوتون و سرعت نور بدست ميآيد:اگرچه همانطور كه بعدا خواهيم ديد، مساله مقياس طول در تئوري ريسمان به خاطر دوگانگي ريسمانها پيچيده و مشكل شد.






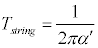

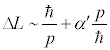
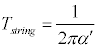
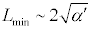
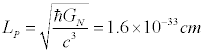




 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (بوک مارک ها)