کانولوشن سیگنال
ارسال شده توسط سعيد اکبری زاده در Saturday, May 29, 2010
در دو مقاله قبلی نشان دادیم که چگونه می توان یک سیگنال دیجیتالی را با استفاده از سیگنال های ضربه تفکیک کرد. سپس مفهوم پاسخ ضربه را بررسی کردیم و دیدیم که هرگونه انتقال و تغییر مقیاس در ورودی موجب همان اندازه انتقال و تغییر مقیاس در خروجی خواهد شد. در این مقاله می خواهیم در عمل نشان دهیم که چگونه می توان با در دست داشتن پاسخ ضربه یک سیستم، خروجی آن سیستم را به ازای هر سیگنال ورودی محاسبه کرد. برای این منظور نیز از عملگری به نام عملگر کانولوشن استفاده خواهیم کرد. همانطور که می دانید هر سیگنال را می توان به شکل یک بردار تصور کرد. با دانستن این نکته می توان حدس زد که منظور از جمع/تفریق دو سیگنال همان جمع/تفریق دو بردار می باشد. به عبارت دیگر عملگر جمع و تفریق با گرفتن دو سیگنال هم اندازه در ورودی خود آن دو را ترکیب کرده و سیگنال خروجی را تولید می کند. فرض کنید پاسخ ضربه یک سیستم نمونه را داریم و می خواهیم به ازای هر ورودی سیگنال، خروجی سیستم را به دست آوریم. واضح است که پاسخ ضربه می تواند هم اندازه با سیگنال ورودی نباشد (در اکثر موارد نیز چنین است ). خروجی نهایی سیستم از کانوالو کردن سیگنال ورودی با پاسخ ضربه سیستم به دست می آید. شکل زیر نشان می دهد که عملگر کانولوشن چگونه بر روی سیگنال ورودی اعمال می شود. فرض کنید سیگنال ورودی X و سیگنال خروجی Y ثابت باشند. درمقابل، ماشین کانولوشن (هرچیزی که داخل کادر خط چین است ) می تواند به چپ یا راست حرکت کند. پس از آنکه ماشین کانولوشن حرکت کرد، مقادیر آن زیر مقادیر سیگنال ورودی قرار می گیرند. سپس چهار نمونه از سیگنال ورودی وارد ماشین کانولوشن شده و با مقادیر نشان داده شده در ماشین کانولوشن (پاسخ ضربه) یک به یک ضرب می شوند. در نهایت نیزجمع کل حاصلضرب ها در نقطه متناظر از سیگنال خروجی قرار می گیرد. به عنوان مثال در شکل نشان داده شده، مقدار y در نقطه 6 در خروجی با استفاده از مقادیر x از 3 تا 6 از سیگنال ورودی محاسبه شده است.
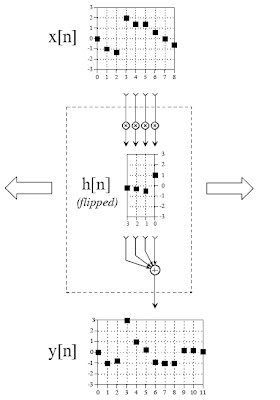
برای محاسبه مقدار y در نقطه 7 ، ماشین کانولوشن یک واحد به سمت راست حرکت کرده و مقادیری از سیگنال ورودی که بالای ماشین کانولوشن قرار دارند وارد ماشین شده و با مقادیر پاسخ ضربه ضرب می شوند در نهایت نیز جمع کل آن ها به عنوان مقدار y در نقطه 7 برگردانده می شود. همین روند برای محاسبه کلیه نمونه های سیگنال خروجی تکرار می شود.
توجه کنید که نحوه چینش مقادیر پاسخ ضربه در داخل ماشین کانولوشن از اهمیت ویژه ای برخوردار است و باید به شکل راست به چپ باشد. راست به چپ کردن مقادیر پاسخ ضربه در داخل ماشین کانولوشن باعث می شود تا مقدار شماره 0 در سمت راست و سایر مقادیر به ترتیب و در سمت چپ آن قرار گیرند. حال که عمگر کانولوشن را توضیح دادیم می توانیم فرموله کردن آن بپردازیم. اگر x سیگنال ورودی با N نمونه از 0 تا N-1 باشد و h نیز سیگنالی M نقطه ای با اندیس 0 تا M-1 باشد کانولوشن این دو، سیگنالی با N+M-1 نمونه است که مقدار آن در هر نقطه به صورت زیر محاسبه می گردد:

در محیط MATLAB از تابع conv برای کانولوشن دو سیگنال می توانیم استفاده کنیم. به عنوان مثال مجموعه دستورات زیر را وارد کرده و نتایج آن مشاهده کنید.
a = 0.5 * sin(2*pi*200/8000*[1:8000]);
plot(a(1:300))
r = rand(1,8000) ./ 10;
plot(r(1:300))
b = a + r;
plot(a(1:300)), hold on, plot(b(1:300),'r')
i = -50:50;
filter = exp( (i .* i) ./ (zeros(1,101)- 18)) ./ (ones(1,101) * (sqrt(2*pi)*3));
plot(filter)
c = conv(b,filter);
wavplay(a)
wavplay(b)
wavplay(c)
plot(a(1:300)), hold on, plot(b(1:300),'r'),plot(c(1:300),'k')
همانطور که در مقاله مربوط به موج سینوسی نشان دادیم، 2 دستور اول موج سینوسی با فرکانس 200 هرتز و نرخ نمونه برداری 8000 نمونه در ثانیه ایجاد می کند. سپس یک سیگنال تصادفی تولید شده و پس از جمع شدن با موج سینوسی، سیگنال جدیدی به دست می آید. در مرحله بعد یک فیلتر گاوسین (شکل روبرو) به اندازه 101 نمونه ایجاد می شود( این همان پاسخ ضربه سیستم را نشان می دهد). در نهایت سیگنال b با فیلتر گاوسین کانوالو شده و سیگنال c تولید می گردد.
زمانی که این سه سیگنال را پخش می کنید متوجه خواهید شد که سیگنال اول یک صدای ایده آل با فرکانس 200 هرتز در خروجی تولید می کند. اما زمانی که سیگنال دوم را پخش می کنید به دلیل افزودن مقادیر تصادفی به آن نویزهایی در خروجی خواهید شنید. نهایتا در سیگنال سوم نیز خواهید شنید که نویزهای سیگنال تا حدود بسیار زیادی از سیگنال نویزدار حذف شده است. در حقیقت حذف نویز به دلیل اعمال پاسخ ضربه گاوسین (فیلتر گاوسین) به سیگنال صورت پذیرفته است.















 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (بوک مارک ها)