قضيه ي فشردگي حدود
قضيه ي فشردگي حدود:
اگرآن گاه :
.(اين قضيه براي حدهاي يك طرفه و بي نهايت هم برقرار است.)
مثال:را بيابيد.
با توجه به شكل زير و استفاده از قضيه ي فشردگي ، نتيجه مي شود كه حد راست برابر 0 است.براي بررسي حد چپ،كافي است نيمه ي ديگر نمودار تابع را در نظر بگيريم كه مشابها" نتيجه مي شود كه حد چپ نيز برابر 0 است و لذا حد مذكور برابر 0 است .
تمرين :حدود زير را بيابيد .(x عددي حقيقي و [y]معرف جز صحيح y است .)











 پاسخ با نقل قول
پاسخ با نقل قول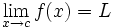 آن گاه این فرمول را چنین میخوانیم << حد تابع f وقتی که x به سمت می رود برابر L است>> توجه کنید که این عبارت حتی اگر
آن گاه این فرمول را چنین میخوانیم << حد تابع f وقتی که x به سمت می رود برابر L است>> توجه کنید که این عبارت حتی اگر 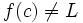
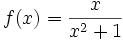
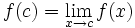 در این صورت گزینه تابع در نقطه X=C دارای
در این صورت گزینه تابع در نقطه X=C دارای 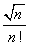 منحنی زرد رنگ در همه جا پیوسته بوده و دارای حد است ولی سه شکل دیگر نمایانگر انواع ناپیوستگی یک نمودار در یک نقطه است
منحنی زرد رنگ در همه جا پیوسته بوده و دارای حد است ولی سه شکل دیگر نمایانگر انواع ناپیوستگی یک نمودار در یک نقطه است 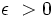 وجود دارد یک
وجود دارد یک  که برای هر x دلخواه اگر
که برای هر x دلخواه اگر 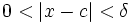 آنگاه نتیجه بگیریم:
آنگاه نتیجه بگیریم: 
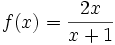 خواهیم داشت:
خواهیم داشت: 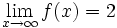
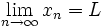 اگر و تنها اگر برای هر
اگر و تنها اگر برای هر 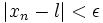
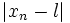 . را به عنوان فاصله بین
. را به عنوان فاصله بین 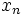 و L در نظر بگیریم به چنین دنباله هایی که حد آنها به یک عدد متناهی میل می کند همگرا گویند و گرنه به آن واگرا گویند.
و L در نظر بگیریم به چنین دنباله هایی که حد آنها به یک عدد متناهی میل می کند همگرا گویند و گرنه به آن واگرا گویند.
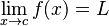
 یک
یک 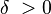 وجود دارد، که برای هر x با خاصیت
وجود دارد، که برای هر x با خاصیت  ، آنگاه داریم:
، آنگاه داریم:  .
. :
: اگر 0 < x < 0 + δ
اگر 0 < x < 0 + δ اگر 0 < x < δ
اگر 0 < x < δ اگر 0 < x < δ
اگر 0 < x < δ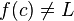 باشد. دو مثال زیر مساله را روشنتر بیان میکند.
باشد. دو مثال زیر مساله را روشنتر بیان میکند. 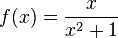 است و به x مقدار ۲ را میدهیم. در این مثال x در ۲ تعریف شده و مقدار تابع در آن برابر حدش ۰٫۴ است:
است و به x مقدار ۲ را میدهیم. در این مثال x در ۲ تعریف شده و مقدار تابع در آن برابر حدش ۰٫۴ است: 0.4
0.4 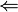 0.3998 0.3988 0.3882 اگر به x مقدار ۲ را بدهیم f(x) برابر ۰٫۴ خواهد شد و داریم
0.3998 0.3988 0.3882 اگر به x مقدار ۲ را بدهیم f(x) برابر ۰٫۴ خواهد شد و داریم  . در این مثال
. در این مثال 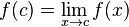 است اما این عبارت همواره صحیح نیست، برای مثال:
است اما این عبارت همواره صحیح نیست، برای مثال: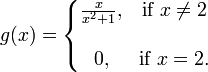
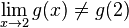 و g در ۲
و g در ۲ 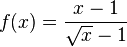



علاقه مندی ها (بوک مارک ها)