در ریاضیات، فرمول انتگرال کوشی، که به احترام آگوستین لوییز کوشی نامگذاری شدهاست، یک حکم اساسی در آنالیز مختلط است و این حقیقت را بیان میکند که یک (تابع هولومورفیک) (Holomorphic function) تعریف شده بر روی یک قرص، به طور کامل با مقادیرش بر روی حاشیهٔ قرص مشخص میشود. این فرمول همچنین میتواند برای ساده کردن انتگرال همهٔ مشتقات یک تابع تحلیلی به کار رود.
فرض کنید U یک زیر مجموعه باز از صفحه مختلط C باشد، و f : U → C یک تابع هلومورفیک باشد، و قرص
D = { z : | z − z0| ≤ r} تماما درون U قرار داشته باشد. و فرض کنید C دایرهای باشد که مرز D را تشکیل میدهد. آنگاه برای هر a در درون D داریم :
که انتگرال کانتور (contour integral) در جهت پادساعتگرد گرفته شدهاست.
اثبات این حکم از قضیهٔ انتگرال کوشی استفاده میکند و مانند آن قضیه فقط به مشتقپذیر بودن f نیاز دارد. از فرمول میتوان نتیجه گرفت که f در حقیقت باید بینهایت بار به طور پیوسته مشتقپذیر باشد، با
برخی این عبارت را فرمول مشتقگیری کوشی مینامند. یک اثبات برای آن، نتیجهٔ فرعی این قضیهاست که توابع هولومورفیک تحلیلیاند.
میتوان دایرهٔ C را با هر منحنی تصحیحپذیر بسته در U که هیچ تقاطعی نداشته باشد و پادشاعتگرد جهتدار باشد جایگزین کرد. فرمول برای هر نقطهٔ a از ناحیهٔ احاطه شده توسط این مسیر معتبر باقی میماند. علاوه بر این، فقط در مورد قضیهٔ انتگرال کوشی، کافیست که f در ناحیه باز احاطه شده توسط منحنی، تحلیلی و بر حاشیهٔ آن پیوسته باشد.
این فرمولها میتوانند برا اثبات قضیه مانده (residue theorem) استفاده شوند، که یک تعمیم وسیع است.
با استفاده از قضیه انتگرال کوشی میتوان نشان داد که انتگرال بر روی C (یا منحنی بستهٔ تصحیحپذیر) برابر است با انتگرال مشابهی که بر روی یک دایرهٔ بسیار کوچک دور a گرفته شدهاست. مادامی که f(z) پیوستهاست، میتوانیم دایرهای به قدر کافی کوچک انتخاب کنیم که f(z) بر روی آن تقریباً ثابت و برابر f(a) باشد. آنگاه باید انتگرال :را بر روی این دایرهٔ کوچک حساب کنیم. این انتگرال با استفاده از تغییر متغیر قابل حل است. قرار دهید
که در آن
و
. این نشان میدهد که مقدار این انتگرال مستقل از شعاع دایره و برابر 2πi است.









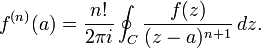

 پاسخ با نقل قول
پاسخ با نقل قول


علاقه مندی ها (بوک مارک ها)